Critics love behavioral economics because they think it gives traditional economics the comeuppance it deserves, and this is a mistake.
The Game Theory Glitch in A Beautiful Mind
Thinking about the economics of Moneyball lead me to think about the film (and book) A Beautiful Mind, about John Nash. Nash won the Nobel Memorial Prize in Economics in 1994 for his contributions to game theory. It’s a fine film. Still, as most adaptations do, the film differs from the book in several important ways. In the book, for example, Nash’s dissertation advisor tells him that his dissertation is trivial, which is a high insult in mathematics. In the film Nash’s advisor tells him his dissertation is revolutionary. The most annoying problem with the film adaptation, however, is in the one and only scene illuminating the application of game theory in the film, the bar scene, the solution the Nash character provides to the game is not a Nash equilibrium.
First, to clear away some brush. There’s a lot of special pleading regarding the scene in the blogosphere: Arguments that the film doesn’t claim the Nash character seeks to provide a Nash equilibrium to the game, that it’s a sequential game rather than a simultaneous game, that he’s trying to outwit his friends so that he can get the blonde, yadda, yadda, yadda. I don’t buy any of it. In the context of the film, the bar scene is supposed to illustrate the equilibrium concept Nash developed, that is, a Nash equilibrium.
So, in the scene, a group of women come into the bar in which Nash sits with a group of his friends who are all men. The group of women include one blonde woman, and the rest are brunettes. Nash and all his friends prefer to pair with the blonde relative to the brunettes, but prefer to pair with one of the brunettes relative to not pairing up at all. As Nash explains it, if all the men approach the blonde first, none of the men will pair off: The blonde will reject them all as a crowd, and her brunette friends will reject them all individually because none of the women will accept being second choice to her friend.
This is a simple version of a congestion game, that is, a game in which several actors pursue the same objective, but in pursuing that objective the actors can deprive themselves of the goal because, under certain contingencies, congestion can prevent the achievement of their objective. Say, for example, several aid agencies want to get relief supplies to a remote region after a natural catastrophe. But infrastructure after the catastrophe is constrained. To wit, if all of the aid agencies attempt to use the single serviceable road leading to the region, or if all attempt to use the single small airport, congestion prevents the agencies from delivering all the aid they have in timely manner.
Back to the game in the film. The game in the bar scene can be simplified to a two-person game. To wit, there are two men, who are the strategic actors in Nash’s story, and a group of women, one of whom is blonde, the others are brunettes. Both men prefer the blonde to the brunettes, but prefer a brunette to being alone. If both men approach the blonde, both men will remain alone. If both men approach a (different) brunette, then each will enjoy the company of that person. If one man approaches the blonde while the other approaches a brunette then, again, each will enjoy the company of that individual.
The Figure below represents this as a simple 2×2 game. A Nash equilibrium exists when none of the players can do better (i.e., receive a higher payoff) by changing to another strategy given the strategy the other player is playing. I make the players’ payoffs cardinal rather than ordinal simply for concreteness; we could use any numbers consistent with the players’ ordinal ranking of the outcomes.
First, note the strategy combination for the boys identified in the film — that both go for brunettes — is not an equilibrium. Each boy have the same incentive to deviate from going for a brunette given the conjecture that the other boy is going for a brunette. To wit, each has the incentive to deviate from the conjectured brunette-brunette strategy combination to approach the blonde. Note we are talking about individual incentives. Both has the incentive to deviate given the symmetry of the game, but we’re talking about one player at a time having the incentive to deviate from a brunette to the blonde given the conjecture that the other player is approaching a brunette.
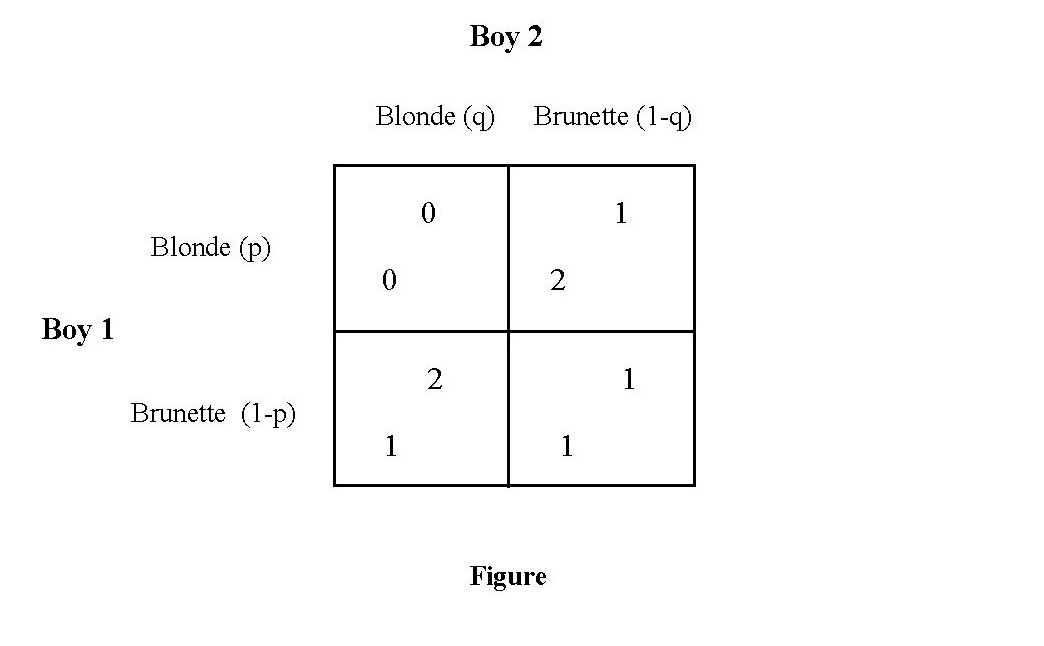
There are three Nash equilibria to the same, two pure-strategy equilibria, and one mixed-strategy equilibrium. (Strategies in pure strategy equilibria are played with probability 1 or zero; strategies in mixed-strategy equilibria are played with probabilities less than one but greater than zero.) The two pure strategy equilibria are mirrors of each other. One of the boys pairs with the blonde, the other boy pairs with a brunette. Both of these strategies are (Pareto) efficient, that is, there is no outcome in the game in which one player can do better without the other player doing worse. The mixed-strategy equilibrium exists with both players “mixing” between the strategies with probability one half (0.5). (This is the “p” and the “q” in the figures.) Expected payoffs for each player in the mixed-strategy equilibrium is “1.” So this is an inefficient equilibrium.
It is the nature of the equilibria that presents the problem that the film’s narrative attempts to solve. First, having multiple equilibria is a problem. The boys might agree that one of them should end up with the blonde, and so agree they should coordinate their actions. But there is a distributive tension between the players. They might argue over which one of them ends up with the blonde and which “settles” for a brunette. Or they might just flip a coin and easily coordinate on a single equilibrium. They need a coordination mechanism of some sort, however.
If we consider the class of congestion game more broadly, again considering the case of aid agencies rushing to get assistance to a remote region, there are incentives for the aid agencies to coordinate in advance: for one agency to send in aid via the road, for the other agency to send in aid via the airport.
But a distributive tension exists here as well, despite the altruistic aims of the agencies. Perhaps the agency to get assistance in first — the agency that sends in aid via airplanes — better achieves the agency’s goal of helping people. But both agencies are passionate about that.
Or, perhaps, being the first agency to deliver assistance in the crisis will boost that agency’s visibility to potential donors and thereby increase its fundraising success. And the more funds the agency raises the better able it is to assist more people. The point being that even among altruistically motivated agents, distributive tensions can threaten coordination. Given this tension, perhaps the mixed-strategy equilibrium is the most plausible of the three equilibria for the game, despite being the only inefficient equilibrium.
The faux-equilibrium identified in the film would seem to integrate the element of envy. To wit, which strategy combination is envy-proof. The film’s solution — all the boys going for brunettes — would satisfy that concept. But adding that to the game requires a different payoff structure from the one explained in the film. The thing is, for a more general congestion game, we don’t want both aid agencies settling for the brunettes. We want aid to start reaching the victims as soon as possible, irrespective of whether the second-arriving aid agency envies the agency with access to the airport. Even with some trussing up, the film’s solution to the game remains unsatisfying.

